Superkavitation in der Natur

In einem ausführlichen Artikel (Bild der Wissenschaft,1974,11, S.60 - 65) beschreibt Helmut Tributsch die Technik der Tölpel anhand ausgezeichneten Bildmaterials. Für die freundliche Genehmigung seine Abbildungen an dieser Stelle zu verwenden sei herzlich gedankt.

Die Abbildung zeigt den stromlinienförmigen Kopf des Tölpels mit seinem langen massiven Schnabel. Auffällig im ersten Drittel des Schnabels ist die kreisförmige Ausführung des oberen Schnabelteils und eine Einschnürung des unteren Schnabelteils nach einem zunächst geradlinigen Verlauf.

Betrachten wir nun die nächste Abbildung. Sie zeigt in Serien-Aufnahme den Sturzflug eines Tölpels

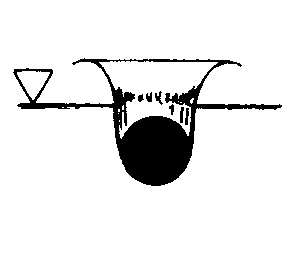
Aus dem freien Flug stürzt er sich ins Wasser, nachdem er sein Angriffsziel ausgemacht hat. Entscheidend sind die letzten beiden Bildphasen. Die vorletzte zeigt den schlanken spindelförmigen Körper kurz vor dem Eintauchen. Die letzte zeigt den Tölpel kurz nach den Eintauchen.

Was geschieht in dieser Phase des Eintauchens?

Die geschlossene Schnabelspitze des Tölpels berührt die Wasseroberfläche und beschleunigt das im Wege befindliche Wasser quer zu seiner Bewegungsrichtung nach außen bis der Schnabel ca. ein Drittel seiner Länge eingetaucht ist. Die Krümmung am oberen Teil des Schnabels und die Einschnürung am unteren Teil bewirken an diesen Stellen eine Ablösung der Wasserströmung, so dass der Tölpel in der weiteren Eintrittsphase praktisch nur mit dem vorderen Drittel seines Schnabels das Wasser berührt.

Für die weitere Berechnung von Eintauchblase und Bewegungsverhalten des Tölpels reicht es, die mit dem Wasser in Berührung stehende Schnabelspitze durch einen Kegel mit Öffnungswinkel 45° und Kegelhöhe = 1/3 Schnabellänge anzunähern.

Nimmt man eineEintauchgeschwindigkeit von 25 m/s an, so ergibt sich nach den Reichardt' schen Blasenformeln (sh. entspr. Kapitel) ein Widerstand, der nahezu identisch mit dem Gewicht des Tölpels ist. Der Widerstand in der Eintrittsphase wird also durch die wirkende Schwerkraft annähernd kompensiert, so dass keine wesentliche Verzögerung erfolgen sollte. Wie kommt es dann zur Spreizung der Schwanzfedern in der Eintauchphase?

Um dies zu verstehen muß man mehr über die Entstehung der Eintauchblase wissen. Im Anhang ist ein Artikel wiedergegeben, der ein Verfahren zur empirischen Berechnung von Eintauchblasen erläutert. Hierfür werden die Reichardt'schen Formeln und ein beliebiges Tabellenkalkulationsprogramm benötigt. Führt man eine derartige Rechnung aus, so erhält man einen sich bildenden schlauchförmigen Eintauchkanal, der sich mit nachströmender Luft aus der Atmosphäre auffüllt. Diese nachströmende Luft muß den spindelförmigen Tölpel umströmen und spreizt dabei die leichten Schwanzfedern.

Der zunächst noch offene Eintauchkanal schnürt sich nach kurzer Zeit im mittleren Bereich ein. Es bildet sich eine geschlossene Blase um den Tölpel, die sich mit zunehmender Tiefe verkleinert, wobei die mittransportierte Luft komprimiert wird, und eine aufsteigende Blase, die beim Zusammenfall an der Oberfläche einen senkrechten Wasserstrahl in die Luft schießt.

Die Evolution hat dem Tölpel zu seiner genialen Fangmethode verholfen. Muß die Menschheit auf die Evolution unserer Schiffbauer hoffen oder gelingt es uns, eine neue Generation von fantasievollen, vorurteilsfreien Schiffbauern auszubilden, die uns innerhalb der nächsten Generation das superkavitierende Schiff bauen, das mit halbierter Antriebsleistung doppelte Geschwindigkeit erreicht?